The Mission
The year is 1988 and two young men stare intently at a computer screen, as a tiny flashing dot haltingly scans the screen left to right and top to bottom. This travelling dot mostly leaves the screen painted in plain chunks of blue, green, and cyan. Occasionally the dot renders an excitingly variegated group of color pixels. It’s past midnight on a frigid evening during my second semester at university. The bay window in the third floor dorm room is cracked open and frosty, invigorating air gusts in. Not wanting to disturb my sleeping roommate, the desk, books, and scattered paper is lit only by the computer screen. I’m sitting close to a new computer with another young man as we intently watch the tiny dot render the fruits of our labors. We are on a mission.
The new computer is on loan to me by my employer. It is a brand new IBM PS/2 Model 60. This computer has a fast CPU and is the first generation of personal computers able to display photograph-like images.
The young man sitting next to me is James, one of the smartest people I have ever met. At 16, he was taking Masters level math classes. I have this special computer and am an accomplished programmer. There are no libraries to make use of this amazing new computer. To coax images from it, you must directly program the underlying hardware, and I could do that.
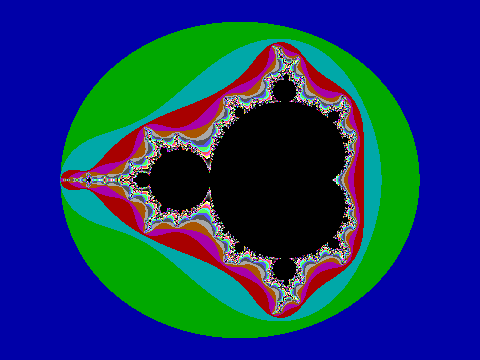
James and I had discussed our plans from the day I found out about the computer loan. Our self-assigned mission: to draw the Mandelbrot set, a colorful and infinitely complex image that mathematicians only recently understood, and then only with the help of computers. Deceptively simple equations describe it. James understood the math and I understood the computer. We started working after class that day. James explained the math and I translated the equations on paper into something the computer could process.
Understand that this is before Google, before the World Wide Web, even before the Internet. The resources we had were a couple math books, a couple books on computer programming, and each other. There was no one to double-check with; there was no one to ask for advice. There were some false starts, and more than once we got colorful static on the screen. This was hard.
Now we have it right. The blinking dot moves quickly through the blue, green, and cyan areas. It frustratingly slows to a crawl in the areas of variegated color and black central to the image. It takes minutes to render each horizontal sliver of the screen. Wide eyed, we stare intently at the screen for over an hour, our vigil only interrupted only by brief, soft discussion of what we are seeing. Exhausted and knowing it will take many hours to complete, we turn off the screen to prevent burn-in and each wearily heads to bed.
When I open my eyes, it is late morning. It takes a few groggy moments to realize that I overslept my first class – and then I remember why! Jumping out of the top bunk, I switch the computer monitor on. There it is. THERE IT IS! Wanting to share the success, I tear myself away from the computer, rush to James’ room and pound on the door. Excitedly, I tell him that the program finished and that IT WORKED! Together we run the short distance back to my room. We both stare at the screen: the image is amazing, more complex than anything I have ever seen.
Looking back, I struggle to describe that morning’s sense of wonder and accomplishment. Both James and I had seen images of the Mandelbrot set in a book. There is a world of difference between seeing the image and being able to reproduce something on the cutting edge of mathematics that had previously been rendered by a famous mathematician with the resources of IBM at his disposal. We were 16 and 17, and we felt as if nothing was beyond our reach.

Recent Comments