Oct 6, 2015 | History, Humanitarian, Science
Norman Borlaug received a Ph.D. in plant pathology and genetics from the U. of Minnesota. He was acutely aware of starvation in the world due to food shortages. Norman worked for more than a decade cross-breeding wheat to grow quickly, be disease resistant, and have shorter, thicker stems. During these years, he and his team created more than 6,000 varieties of wheat. Norman realized that many areas suffering chronic food shortages were equatorial or semi-equatorial. This meant that there was enough sunlight to have two growing seasons, increasing crop yields by 40%. Norman bred for disease resistance and planted each field with multiple varieties of wheat. These different varieties in a field mean that while disease might wipe out one or a few of the varieties, other varieties were likely to survive, meaning the farmer and his family would have both food and income from the season.
Critically, Norman bred for short, thick stems that give his wheat the name dwarf wheat. Traditional wheat is tall and thin to better catch the sunlight in temperate latitudes. Sunlight is plentiful in tropical and sub-tropical latitudes, and the thicker stalks supported more grain per plant. The shorter, thicker stalks of dwarf wheat also resisted pouring tropical rains that snapped the thinner stalks of conventional wheat.
In the 1960s, the Indian subcontinent was experiencing food shortages so severe that the U.S. was making annual grain shipments (exceeding 20% of the total U.S. harvest) to the region to prevent mass starvation. Norman’s initial efforts on the subcontinent were blocked by local bureaucracies and cultural opposition to new ways of agriculture. In 1965, the famine had grown so acute that the national governments stepped in and allowed his projects to go forward. Norman and his team began planting immediately, despite often in sight of artillery flashes from the war between India and Pakistan over the Kashmir region that started the same year.
The initial yields of Borlaug’s crops were higher than any ever harvested in South Asia. By 1968, Pakistan was self-sufficient in wheat production. High yields led to a shortage of various utilities — labor to harvest the crops, bullock carts to haul it to the threshing floor, jute bags, trucks, rail cars, and grain storage facilities. Some local governments were forced to close school buildings temporarily to use them for grain storage.[16] Not only did the high yields prevent starvation, they also protected the environment. India’s use of high-yield farming has prevented an estimated 100 million acres (400,000 km²) of virgin land from being converted into farmland—an area about the size of California, or 13.6% of the total area of India.[30]
Norman Borlaug won the Nobel Peace Prize in 1970, yet this seems pale in comparison to what he accomplished.
How does one measure the life of a man? For tyrants of the 20th century, we catalog their horrors by the number of dead. Perhaps, then, counting lives saved is an appropriate metric for those who work on the side of angels. What does it mean when a person saves one thousand lives? A medical doctor may do this every few years. What about one million lives? A rare politician may do this once in their career. How about one billion lives? That is 1,000,000,000 people. One billion people consisting of mothers and daughters, fathers and sons, husbands and wives, doctors, lawyers, scientists… The scope and scale of saving a billion lives beggars human imagination. Yet a man named Norman Borlaug saved at least one billion lives from the horrors of starvation.
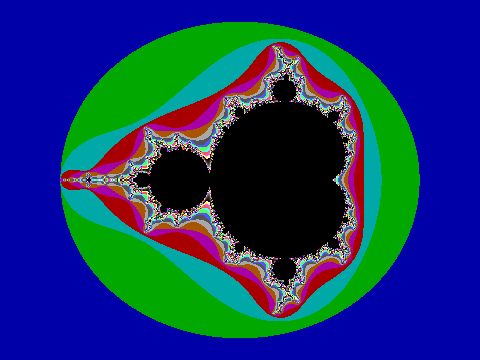
Oct 2, 2015 | Math
The year is 1988 and two young men stare intently at a computer screen, as a tiny flashing dot haltingly scans the screen left to right and top to bottom. This travelling dot mostly leaves the screen painted in plain chunks of blue, green, and cyan. Occasionally the dot renders an excitingly variegated group of color pixels. It’s past midnight on a frigid evening during my second semester at university. The bay window in the third floor dorm room is cracked open and frosty, invigorating air gusts in. Not wanting to disturb my sleeping roommate, the desk, books, and scattered paper is lit only by the computer screen. I’m sitting close to a new computer with another young man as we intently watch the tiny dot render the fruits of our labors. We are on a mission.
The new computer is on loan to me by my employer. It is a brand new IBM PS/2 Model 60. This computer has a fast CPU and is the first generation of personal computers able to display photograph-like images.
The young man sitting next to me is James, one of the smartest people I have ever met. At 16, he was taking Masters level math classes. I have this special computer and am an accomplished programmer. There are no libraries to make use of this amazing new computer. To coax images from it, you must directly program the underlying hardware, and I could do that.
James and I had discussed our plans from the day I found out about the computer loan. Our self-assigned mission: to draw the Mandelbrot set, a colorful and infinitely complex image that mathematicians only recently understood, and then only with the help of computers. Deceptively simple equations describe it. James understood the math and I understood the computer. We started working after class that day. James explained the math and I translated the equations on paper into something the computer could process.
Understand that this is before Google, before the World Wide Web, even before the Internet. The resources we had were a couple math books, a couple books on computer programming, and each other. There was no one to double-check with; there was no one to ask for advice. There were some false starts, and more than once we got colorful static on the screen. This was hard.
Now we have it right. The blinking dot moves quickly through the blue, green, and cyan areas. It frustratingly slows to a crawl in the areas of variegated color and black central to the image. It takes minutes to render each horizontal sliver of the screen. Wide eyed, we stare intently at the screen for over an hour, our vigil only interrupted only by brief, soft discussion of what we are seeing. Exhausted and knowing it will take many hours to complete, we turn off the screen to prevent burn-in and each wearily heads to bed.
When I open my eyes, it is late morning. It takes a few groggy moments to realize that I overslept my first class – and then I remember why! Jumping out of the top bunk, I switch the computer monitor on. There it is. THERE IT IS! Wanting to share the success, I tear myself away from the computer, rush to James’ room and pound on the door. Excitedly, I tell him that the program finished and that IT WORKED! Together we run the short distance back to my room. We both stare at the screen: the image is amazing, more complex than anything I have ever seen.
Looking back, I struggle to describe that morning’s sense of wonder and accomplishment. Both James and I had seen images of the Mandelbrot set in a book. There is a world of difference between seeing the image and being able to reproduce something on the cutting edge of mathematics that had previously been rendered by a famous mathematician with the resources of IBM at his disposal. We were 16 and 17, and we felt as if nothing was beyond our reach.


Recent Comments